The Three-Body Problem: by Liu Cixin is a science fiction novel about chaos theory

The chain he found did not converge. That is, the sum does not approximate a unique function corresponding to the path of an object. In order to avoid possible conflicts with the king and other experts, Mittag-Leffler decided to present the award to Poincaré anyway. However, he was supposed to improve his work and pay the printing costs already incurred (which amounted to 3,500 kroner, i.e. 1,000 more than the prize money itself). While Poincaré was doing his calculations, he realized the reason for the lack of convergence: the three-body systems he was studying behaved chaotically.

Chaos spoils everything

This does not mean that the three masses do not follow fixed rules. Of course, they are still subject to gravity and follow a path resulting from mutual attraction. But: the smallest changes in the system can have huge impacts. “If you knew the paths of a three-star system and changed the location of one of them by just a few millimeters, the paths could suddenly be completely different,” mathematician Richard Montgomery said in an article published in the journal “Spectrum Science.” At the University of California, Santa Cruz, he is researching this topic.

For example, let us consider three objects that always form a straight line and move through space, as in Euler’s original description. Let’s say you want to move a corpse slightly, for example, because an asteroid hit it. As a result, the entire system would suddenly follow a completely different dynamic, and blocks would be randomly grouped together – and eventually one of them would probably leave the system and disappear into the depths of space. Realizing that the smallest changes in a system can have major consequences, Poincaré is considered one of the founders of chaos theory. In Liu Cixin’s novel, this chaos is also responsible for the fact that the movements of the three stars cannot be accurately predicted – and why the Trisolarians need a new home planet.

Therefore the Poincaré approach was not able to solve the task set by Mittag-Leffler: developing a convergent series for the three-body problem. In 1912, Finnish mathematician Karl Frithiof Sandmann achieved this masterpiece. He gave an infinite sum corresponding to the trajectories of masses in the general three-body problem. This solves the problem, doesn’t it? Unfortunately not quite. The series converges very slowly. As it turns out, you’ll do about 10^8,000,000 (one followed by eight million zeros) Calculate the terms before obtaining a reliable result. Unfortunately, in practice the result is useless.

The development of computers opened up entirely new possibilities for tackling the three-body problem. Experts were now able to search for numerically related solutions: by roughly solving differential equations using algorithms, they achieved amazing results. This is what mathematician Chris Moore discovered in 1993 A fixed, constrained solution for three equal masses: These masses chase each other along a curve that has the shape of an 8 (or infinity symbol).

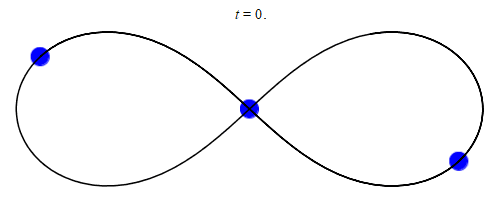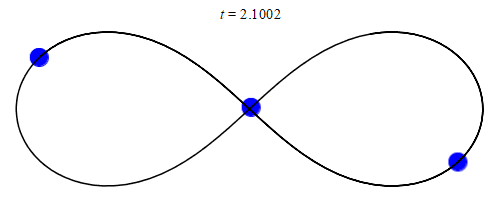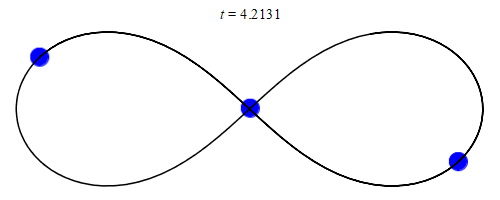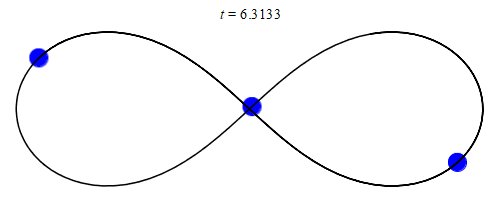
20 years later, it was discovered by physicists Milovan Šovakov and Veljko Dmitrasinović. 13 more restrictive solutions The three-body problem, discovered by Anna Hodomal in 2015 14 new Three years later, Xiaoming Li and Shijun Liao made their calculations A total of nearly 2000 solutions. Efforts have reached their peak so far in 2023, when Ivan Hristov, Radoslava Hristova, Dimitrasinovich, and Kiyotaka Tanikawa have found more than 12,000 new solutions to the three-body problem, thanks to the help of supercomputers.

However, it is questionable how relevant all these solutions are for real systems. Researchers have not yet been able to prove whether the systems are stable. However, if we encounter triple star systems in space, these systems must conform to stable shapes, otherwise they will quickly break apart again. But who knows: perhaps we will soon observe an octagonal path of three stars chasing each other. It is unclear whether a planet in such a solar system could develop conditions suitable for life. But unlike the Trisolarians in Liu Cixin’s novel, the dynamics of the system can at least be predicted.